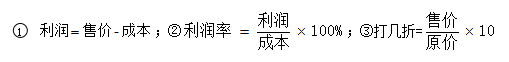在行测考试中,数量关系经常考查利润问题,其重要性不言而喻。那么,今天小编教大家从一场小本买卖看清利润问题!
一、计算关系
张大爷爱好养鱼,现在以2元一条的价格购入。李大爷登门拜访,对小鱼甚是心喜,就打算向张大爷买。张大爷报价10元一条。李大爷大砍价,以5元一条买回了家。
这个小故事当中,对于张大爷而言,就像是做了一场小本买卖,一条小鱼成本是2元,标价是10元,实际售价是5元,赚得利润是5-2=3元,虽然钱数不多,但是利润率很高啊。原价10元,实际售价5元,相当于五折。此时我们学习了三个公式:
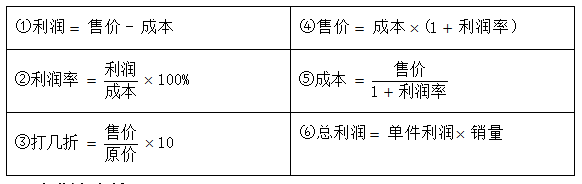
那如果李大爷买走的不是一条鱼,而是以5元的单价买走了六条鱼,此时张大爷从这6条鱼中赚了多少呢?一条赚3元,六条赚18元。所以这就是一个新的计算关系:
总利润=单件利润×销量
二、技巧总结
三、例题讲解
例题1、某商品按定价出售,每个可获得60元的利润。按定价打八折出售10个所获得的利润,与按定价每个减价30元出售15个所获得的利润相同。该商品的定价为多少元?
A.75
C.80
B.85
D.90
【答案】A。解析:本题给出了明确的描述“按定价打八折出售10个所获得的利润,与按定价每个减价30元出售15个所获得的利润相同”,由此我们得到两种销售情况的总利润相等。第一种情况,定价x元,因为原定价每个可获利60元,所以成本为x-60元。打八折售价为0.8x,单件利润=售价-成本=0.8x-(x-60)=60-0.2x。销售10件,总利润=单件利润×销量=(60-0.2x)×10;第二种情况,每个减价30元,则原来60元的利润少30元,单件利润为(60-30)=30元。销量15件,总利润=单件利润×销量=30×15=450元,因为两种情况总利润相等,所以列出方程(60-0.2x)×10=450,解得x=75,选A。
例题2、小李四年前投资的一套商品房价格上涨了50%,由于担心房价下跌,他将该商品房按市价的9折出售,扣除成交价5%的相关交易费用后,比买进时赚了56.5万元。那么,小李买进该商品房时花了多少万元?
A.200
B.300
C.250
D.350
【答案】A。解析:设买进成本x万元,上涨50%则市场价1.5x,9折出售则成交价0.9×1.5x,“扣除成交价5%的相关交易费用”说明成本当中包括了5%×0.9×1.5x的交易费,而赚了56.5万元,售价-成本=利润,列式0.9×1.5x-(x+5%×0.9×1.5x)=56.5,解方程得x=200,选A。
利润问题,往往需要我们把买卖的钱数关系梳理清楚,最后依据等量关系求解。它需要一定的熟练程度才能提高解题速度。所以,要多找找题目进行强化练习哦!


 更多行测技巧与方法扫码获取
更多行测技巧与方法扫码获取